题目内容
【题目】如图,点D,C在BF上,AC∥DE,∠A=∠E,BD=CF.
(1)求证:AB=EF;
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
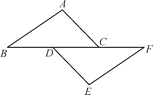
【答案】(1)证明见解析;(2)四边形ABEF为平行四边形,理由见解析.
【解析】(1)利用AAS证明△ABC≌△EFD,再根据全等三角形的性质可得AB=EF;
(2)首先根据全等三角形的性质可得∠B=∠F,再根据内错角相等两直线平行可得到AB∥EF,又AB=EF,可证出四边形ABEF为平行四边形.
解:(1)证明:∵AC∥DE,
∴∠ACD=∠EDF,
∵BD=CF,
∴BD+DC=CF+DC,
即BC=DF,
又∵∠A=∠E,
∴△ABC≌△EFD(AAS),
∴AB=EF;
(2)猜想:四边形ABEF为平行四边形,
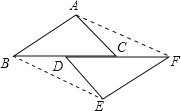
理由如下:由(1)知△ABC≌△EFD,
∴∠B=∠F,
∴AB∥EF,
又∵AB=EF,
∴四边形ABEF为平行四边形.
“点睛”此题主要考查了全等三角形的判定与性质,平行四边形的判定,解决问题的关键是证明△ABC≌△EFD.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】为了对学生进行多元化的评价,某中学决定对学生进行综合素质评价![]() 设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
中学生综合素质评价成绩 | 中学生综合素质评价等级 |
| A级 |
| B级 |
| C级 |
| D级 |
现随机抽取该校部分学生的综合素质评价成绩,整理绘制成图![]() 、图
、图![]() 两幅不完整的统计图
两幅不完整的统计图![]() 请根据相关信息,解答下列问题:
请根据相关信息,解答下列问题:
(1)在这次调查中,一共抽取了______名学生,图![]() 中等级为D级的扇形的圆心角
中等级为D级的扇形的圆心角![]() 等于______
等于______![]() ;
;
(2)补全图![]() 中的条形统计图;
中的条形统计图;
(3)若该校共有1200名学生,请你估计该校等级为C级的学生约有多少名.