题目内容
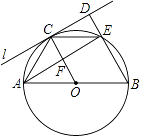
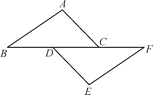
【题目】如图，在四边形ABCD中，
，
，
，
，E是BC的中点，P是AB上的任意一点，连接PE，将PE绕点P逆时针旋转
得到PQ，过A点，D点分别作BC的垂线，垂足分别为M，N．
求AM的值；
连接AC，若P是AB的中点，求PE的长；
若点Q落在AB或AD边所在直线上，请直接写出BP的长．
【答案】（1）12；（2）10；（3）PB的值为
或
．
【解析】
作等腰梯形的双高，把问题转化为矩形，全等三角形即可解决问题；
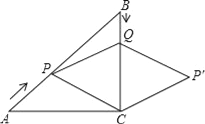
如图2中，连接
利用勾股定理求出AC，再利用三角形的中位线定理求出PE；
分两种情形分别讨论求解即可解决问题.
如图1中，作
用M，
于N．
，
，
，
四边形AMND是矩形，
，
，
≌
，
，
，
，
，
，
如图2中，连接AC．
在
中，
，
，
，
，
如图3中，当点Q落在直线AB上时，
∽
，
，
，
．
如图4中，当点Q在DA的延长线上时，作
交DA的延长线于H，延长HP交BC于G．
设
，则
．
，
，
，
，
，
≌
，
，
，
．
综上所述，满足条件的PB的值为或．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】阅读下面材料：
小明想探究函数
的性质，他借助计算器求出了y与x的几组对应值，并在平面直角坐标系中画出了函数图象：
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
小聪看了一眼就说：“你画的图象肯定是错误的．”
请回答：小聪判断的理由是_____________．请写出函数的一条性质：_____________．
