Question

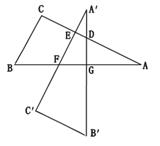
如图所示，直角三角板ABC的两直角边AC、BC的长分别为4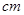0和30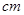，点G在斜边AB上，且BG＝30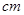，将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置，那么旋转前后两个三角板重叠部分（四边形EFGD）的面积为           .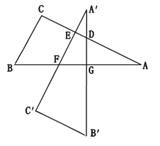

Answer 1

144cm²

解析试题分析：把所求重叠部分面积看作△A′FG与△A′DE的面积差，并且这两个三角形都与△ABC相似，根据勾股定理求对应边的长，根据相似三角形的面积比等于相似比的平方求面积即可．

又∵BG=30，
∴AG=AB-BG=20，

解得DG=15，AD=25，
A′D=A′G-DG=AG-GD=20-15=5，

根据相似三角形面积比等于相似比的平方，可知

考点：旋转的性质，勾股定理、相似三角形的判定和性质
点评：相似三角形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.