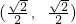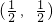题目内容
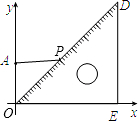
 把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,已知动点P在斜边OD上运动,点A的坐标为(0,
把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,已知动点P在斜边OD上运动,点A的坐标为(0,| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
分析:由点A到OD的距离,即点A到OD的垂线段,这也是最短的,由已知特殊角和点的坐标即求得.
解答: 解:如图,作AB⊥OD于点B点,BC⊥OE于点C.
解:如图,作AB⊥OD于点B点,BC⊥OE于点C.
把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,
由三角板的特点,都有一角为90°,
∴∠AOD=∠BOE=45°,
∴另一角也是45°.
则在Rt△AOB中,由点A坐标知道OA=
,
∴OB=OAcos45°=
×
=1.
在Rt△OBC中,BC=OC=OBsin∠BOE=
,
∴B(
,
),
点B即为点A到OD距离最短时的点P.
∴点P(
,
).
故选B.
 解:如图,作AB⊥OD于点B点,BC⊥OE于点C.
解:如图,作AB⊥OD于点B点,BC⊥OE于点C.把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,
由三角板的特点,都有一角为90°,
∴∠AOD=∠BOE=45°,
∴另一角也是45°.
则在Rt△AOB中,由点A坐标知道OA=
| 2 |
∴OB=OAcos45°=
| 2 |
| ||
| 2 |
在Rt△OBC中,BC=OC=OBsin∠BOE=
| ||
| 2 |
∴B(
| ||
| 2 |
| ||
| 2 |
点B即为点A到OD距离最短时的点P.
∴点P(
| ||
| 2 |
| ||
| 2 |
故选B.
点评:本题考查了解直角三角形,由特殊角结合三角函数求边长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,BC长为半径作⊙B,求线段PN与⊙B有一个交点时,t的范围.
,BC长为半径作⊙B,求线段PN与⊙B有一个交点时,t的范围. ,BC长为半径作⊙B,求线段PN与⊙B有一个交点时,t的范围.
,BC长为半径作⊙B,求线段PN与⊙B有一个交点时,t的范围.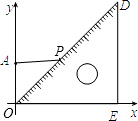 把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,已知动点P在斜边OD上运动,点A的坐标为
把一块含45°的直角三角板ODE放在如图所示的直角坐标系中,已知动点P在斜边OD上运动,点A的坐标为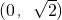 ,当线段AP最短时,则点P的坐标为
,当线段AP最短时,则点P的坐标为