Question

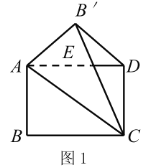
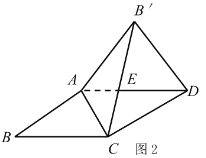
【题目】如图，是正方形的对角线，，边在其所在直线上向右平移，将通过平移得到的线段记为，连结，，并过点作，垂足为，连接和，在平移变换过程中，设的面积为，，则的最大值是________．

Answer 1

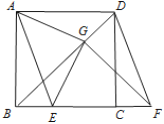
【答案】5

【解析】

证△AGB≌△EGF，得到AG=EG，△AGE是等腰直角三角形，由勾股定理得到AE的长度，再根据三角函数，把AG、GE表示出来，列出面积的方程式，求解可得到答案.

解：∵时正方形，是正方形的对角线，

∴AB=EF, ∠ABD=45°，∠DBC=45°

又∵，

∴△BGF是等腰直角三角形，

∴∠GFE=45°，BG=FG，

∴△AGB≌△EGF（SAS），

∴AG=EG，△AGE是等腰直角三角形，

∵，

∴，

∴

∴

=

又∵，

∴当时，取得最大值5，

故有最大值5.