题目内容
17.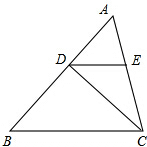 如图.在△ABC中.AB=4,D是AB上的一点(不与点A、B重合),DE∥BC.交于点E.设△ABC的面积为S.△DEC的面积为S′.
如图.在△ABC中.AB=4,D是AB上的一点(不与点A、B重合),DE∥BC.交于点E.设△ABC的面积为S.△DEC的面积为S′.(1)当D是AB的中点时.求$\frac{S′}{S}$的值.
(2)若AD=x,$\frac{S′}{S}$=y,求y关于x的函数关系式以及自变量x的取值范围.
(3)根据y的取值范围,探索S与S′之间的大小关系.并说明理由.
分析 (1)先求出△ADE和△CDE的面积相等,再根据平行线得出△ADE∽△ABC,推出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2,把AB=2AD代入求出即可;
(2)求出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{16}$x2①,$\frac{{S}_{△ADE}}{{S}_{△DEC}}$=$\frac{AE}{EC}$=$\frac{x}{4-x}$②,①÷②即可得出答案;
(3)由(2)知x的取值范围是0<x<4,于是得到y=$\frac{S′}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x=-$\frac{1}{16}$(x-2)2+$\frac{1}{4}$≤$\frac{1}{4}$,即可得到结论.
解答 解:(1)∵D为AB中点,
∴AB=2AD,
∵DE∥BC,
∴AE=EC,
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴S△ADE=S△CDE=S1,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,
∴S′:S=1:4;
(2)∵AB=4,AD=x,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{x}{4}$)2,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{16}$x2①,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∵AB=4,AD=x,
∴$\frac{AE}{AC}$=$\frac{x}{4}$,
∴$\frac{AE}{CE}$=$\frac{x}{4-x}$
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$\frac{{S}_{△ADE}}{{S}_{△DEC}}$=$\frac{AE}{EC}$=$\frac{x}{4-x}$②,
①÷②得:
∴y=$\frac{S′}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x,
∵AB=4,
∴x的取值范围是0<x<4;
(3)由(2)知x的取值范围是0<x<4,
∴y=$\frac{S′}{S}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x=-$\frac{1}{16}$(x-2)2+$\frac{1}{4}$≤$\frac{1}{4}$,
∴S′≤$\frac{1}{4}$S.
点评 本题主要考查了相似三角形的性质和判定,三角形的面积的计算方法,二次函数的最值问题,熟练掌握相似三角形的判定和性质定理是解题的关键.

 如图是由三个圆柱组成的几何体,它的主视图是( )
如图是由三个圆柱组成的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
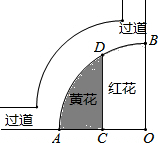 如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π).
如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π). 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明:△OAE≌△OBE.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明:△OAE≌△OBE.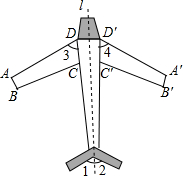 如图是轴对称图形.图中直线1是它的对称轴.
如图是轴对称图形.图中直线1是它的对称轴. 如图,圆柱的体积V=Sh.其中,S为圆柱的底而积,h为圆柱的高.
如图,圆柱的体积V=Sh.其中,S为圆柱的底而积,h为圆柱的高.