题目内容
8. 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明:△OAE≌△OBE.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明:△OAE≌△OBE.
分析 首选证明△CAB≌△DBA可得∠OAB=∠OBA,再根据等角对等边可得AO=BO,然后再证明△OAE≌△OBE即可.
解答 证明:∵在△CAB和△DBA中$\left\{\begin{array}{l}{AC=DB}\\{∠BAC=∠ABD}\\{AB=AB}\end{array}\right.$,
∴△CAB≌△DBA(SAS),
∵∠OAB=∠OBA,
∴AO=BO,
∵点E是AB的中点,
∴AE=BE,
在△AOE和△BOE中$\left\{\begin{array}{l}{AO=BO}\\{EO=EO}\\{AE=BE}\end{array}\right.$,
∴△OAE≌△OBE(SSS).
点评 此题主要考查了三角形全等的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.已知某同学近几次的数学成绩(单位:分)分别为92,90,88,92,93,则该同学这几次数学成绩的平均数和众数分别是( )
| A. | 90分,90分 | B. | 91分,92分 | C. | 92分,92分 | D. | 89分,92分 |
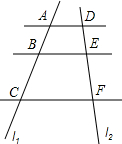 如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值.
如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值.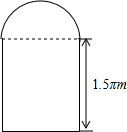 一条隧道的截面如图所示,它的上半部是一个半圆、下半部是一个矩形,矩形一边长为1.5πm,若隧道的截面积为5πm2.求半圆的半径(精确到0.01)
一条隧道的截面如图所示,它的上半部是一个半圆、下半部是一个矩形,矩形一边长为1.5πm,若隧道的截面积为5πm2.求半圆的半径(精确到0.01)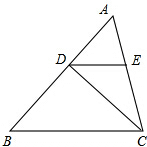 如图.在△ABC中.AB=4,D是AB上的一点(不与点A、B重合),DE∥BC.交于点E.设△ABC的面积为S.△DEC的面积为S′.
如图.在△ABC中.AB=4,D是AB上的一点(不与点A、B重合),DE∥BC.交于点E.设△ABC的面积为S.△DEC的面积为S′.