题目内容
11. 如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F
如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F(1)求证:四边形OECF为正方形;
(2)若AB=6,BC=4,求AC的长和⊙O的半径.
分析 (1)先根据切线的性质得出CE=CF,∠OEF=∠OFC=90°,再由∠C=90°即可得出结论;
(2)连接OA,OB,OC,OD,先根据勾股定理求出AC的长,再设⊙O的半径为r,利用三角形的面积公式即可得出结论.
解答 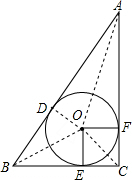 (1)证明:∵BC、AC是⊙O的切线,
(1)证明:∵BC、AC是⊙O的切线,
∴CE=CF,∠OEF=∠OFC=90°.
∵∠C=90°,
∴四边形OECF为正方形;
(2)连接OA,OB,OC,OD,
∵在△ABC中,∠C=90°,AB=6,BC=4,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$.
设⊙O的半径为r,则S△ABC=S△AOC+S△BOC+S△AOB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$(AC+BC+AB)•r,
即8$\sqrt{5}$=(2$\sqrt{5}$+6+4)r,解得r=$\sqrt{5}$-1.
点评 本题考查的是三角形的内切圆与内心,熟知三角形的内心就是三角形三个内角角平分线的交点是解答此题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
2.下列实数中,属于无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{9}$ | C. | 3.14 | D. | $\frac{1}{3}$ |

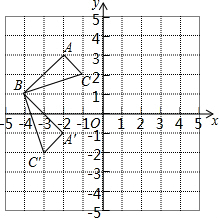 在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题: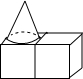 如图,由两个相同的小正方体和一个圆锥组成的几何体,其左视图是( )
如图,由两个相同的小正方体和一个圆锥组成的几何体,其左视图是( )


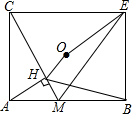 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )