Question

已知：如图，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t≤2），解答下列问题：
（1）当t为何值时，PQ∥BC？
（2）设△AQP的面积为y（cm²），当t为何值时，y最大，并求出最大值．

Answer 1

考点：相似形综合题

专题：

分析：（1）由勾股定理得出AB，因为AP=5-t，AQ=2t，则可证明△APQ∽△ABC，即可求得t；
（2）过点P作PH⊥AC于H．由△APH∽△ABC，得PH=3-

3

5

t，然后根据三角形的面积公式，从而求得y与t的函数关系式．

解答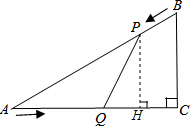：解：（1）在Rt△ABC中，AB=

BC2+AC2

，
由题意知：AP=5-t，AQ=2t，
若PQ∥BC，则△APQ∽△ABC，
∴

AQ

AC

=

AP

AB

，
∴

2t

4

=

5-t

5

，
解得：t=

10

7

．
故当t=

10

7

秒时，PQ∥BC；

（2）如图，过点P作PH⊥AC于H．
∵∠C=90°，
∴AC⊥BC，
∴PH∥BC，
∴△APH∽△ABC，
∴

PH

BC

=

AP

AB

，
∴

PH

3

=

5-t

5

，
∴PH=3-

3

5

t，
∴△AQP的面积为：
y=

1

2

×AQ×PH
=

1

2

×2t×（3-

3

5

t）
=-

3

5

t²+3t
=-

3

5

（t²-5t）
=-

3

5

（t-

5

2

）²+

15

4

，
∵0＜t≤2，
∴当t为2秒时，y最大，最大值为：

18

5

cm²．

点评：此题主要考查了相似三角形的判定与性质以及二次函数的最值问题以及勾股定理等知识，利用相似三角形的性质得出PH的长是解题关键．