题目内容
14.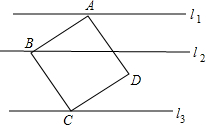 直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2,l3上,l1、l2之间的距离是4,l2,l3之间的距离是5,则正方形ABCD的面积是41.
直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2,l3上,l1、l2之间的距离是4,l2,l3之间的距离是5,则正方形ABCD的面积是41.
分析 画出L1到L2,L2到L3的距离,分别交L2,L3于E,F,通过证明△ABE≌△BCF,得出BF=AE,再由勾股定理即可得出结论.
解答 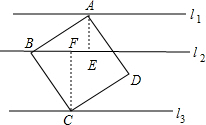 解:过点A作AE⊥l1,过点C作CF⊥l2,
解:过点A作AE⊥l1,过点C作CF⊥l2,
∴∠CBF+∠BCF=90°,
四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴∠ABE+∠CBF=90°,
∵l1∥l2∥l3,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠AEB=∠BFC}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$
∴△ABE≌△BCF(AAS)(画出L1到L2,L2到L3的距离,分别交L2,L3于E,F),
∴BF=AE,
∴BF2+CF2=BC2,
∴BC2=42+52=41.
故答案为:41.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质以及正方形面积的求解方法,能够熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 联结直线外一点到直线上各点的所有线段中,垂线最短 | |
| C. | 经过一点,有且只有一条直线与已知直线平行 | |
| D. | 在同一平面内,经过一点,有且只有一条直线与已知直线垂直 |
3. 如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
 如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50cm的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 300cm2 |
 已知:如图,等腰△ABC中,AB=AC,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别为线段BO和CO中点.求证:四边形EDNM是矩形.
已知:如图,等腰△ABC中,AB=AC,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别为线段BO和CO中点.求证:四边形EDNM是矩形.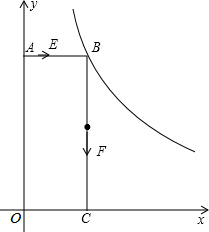 如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.
如图,已知:矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且AB=3,BC=8.