Question

下面是小亮同学做的题目：关于x的方程2kx²+（8k+1）x+8k=0有两个不相等的实数根，求k的取值范围．
∵原方程有两个不相等的实数根
∴b²-4ac＞0，∴（8k+1）²-4×2k×8k＞0，
∴k＞-

1

16

∴当k＞-

1

16

时，原方程有两个不相等的实数根．
以上解法对吗？如有错误，写出正确的解题过程．

Answer 1

错误．
∵原方程有两个不相等的实数根，
∴

k≠0 △=b2-4ac＞0

，即

k≠0 △=(8k+1)2-4×2k×8k＞0

，
∴k＞-

1

16

且k≠0，
∴当k＞-

1

16

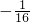且k≠0时，原方程有两个不相等的实数根．