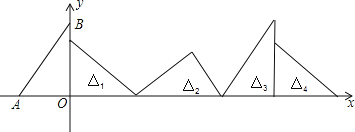
题目内容
【题目】为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格![]() (元/公斤)与第
(元/公斤)与第![]() 天之间满足
天之间满足![]() (
(![]() 为正整数),销售量
为正整数),销售量![]() (公斤)与第
(公斤)与第![]() 天之间的函数关系如图所示:
天之间的函数关系如图所示:
如果李大爷的草莓在上市销售期间每天的维护费用为80元.
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在草莓上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() .
.
【答案】(1)![]() ;(2)
;(2)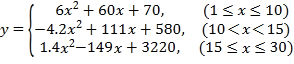 ;(3)草莓销售第13天时,日销售利润
;(3)草莓销售第13天时,日销售利润![]() 最大,最大值是1313.2元
最大,最大值是1313.2元
【解析】
本题是通过构建函数模型解答销售利润的问题.
(1)依据题意利用待定系数法易求得销售量![]() 与第
与第![]() 天之间的函数关系式,
天之间的函数关系式,
(2)然后根据销售利润=销售量×(售价﹣进价),列出每天的销售利润![]() 与第
与第![]() 天之间的函数关系式,
天之间的函数关系式,
(3)再依据函数的增减性求得最大利润.
(1)当![]() 时,设
时,设![]() ,由图知可知
,由图知可知
![]() ,解得
,解得![]() ,
,
![]()
同理得,当![]() 时,
时,![]()
![]() 销售量
销售量![]() 与第
与第![]() 天之间的函数关系式:
天之间的函数关系式:![]()
(2)![]()
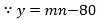 ,
,
整理得,
(3)当![]() 时,
时,
![]() 的对称轴
的对称轴![]()
![]() 此时,在对称轴的右侧
此时,在对称轴的右侧![]() 随
随![]() 的增大而增大
的增大而增大
![]() 时,
时,![]() 取最大值,则
取最大值,则![]()
当![]() 时
时
![]() 的对称轴是
的对称轴是![]()
![]() 在
在![]() 时,
时,![]() 取得最大值,此时
取得最大值,此时![]()
当![]() 时
时
![]() 的对称轴为
的对称轴为![]()
![]() 此时,在对称轴的左侧
此时,在对称轴的左侧![]() 随
随![]() 的增大而减小
的增大而减小
![]() 时,
时,![]() 取最大值,
取最大值,![]() 的最大值是
的最大值是![]()
综上,草莓销售第13天时,日销售利润![]() 最大,最大值是1313.2元
最大,最大值是1313.2元

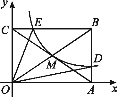
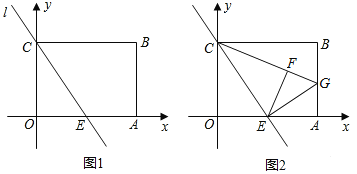
【题目】如图,直线![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]() .
.
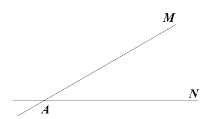
(1)确定点![]() 的位置,在线段
的位置,在线段![]() 上任取一点
上任取一点![]() ,根据题意,补全图形;
,根据题意,补全图形;
(2)设![]() cm,
cm,![]() cm,探究函数
cm,探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
①通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
(要求:补全表格,相关数值保留一位小数)
②)建立平面直角坐标系![]() ,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;

③结合画出的函数图象,解决问题:当![]() 为
为![]() 斜边
斜边![]() 上的中线时,
上的中线时,![]() 的长度约为_____cm(结果保留一位小数).
的长度约为_____cm(结果保留一位小数).
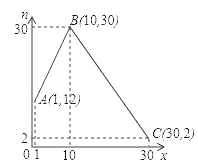
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
时间 |
|
|
售价(元/件) |
| 90 |
每天销量(件) |
| |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元
元
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?