题目内容
如图, O是△ABC的重心, 若△EDO的周长为4,则△AOC的周长为

8
【解析】
试题分析:根据三角形的重心的性质,利用相似三角形的面积比等于相似比的平方,即可求解
【解析】
∵O是△ABC的重心,
∴ ,
,
∴△ODE∽△OAC,
∴△ODE 与△OAC 的周长比等于 ,
,
∴△OAC 的周长是△ODE 的周长的2倍
又∵△ODE的周长为4
∴△OAC 的周长为8
考点:三角形的重心;相似三角形的判定与性质

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 时,代数式
时,代数式 的值为2015,则
的值为2015,则 时,代数式
时,代数式 的值为__________.
的值为__________.

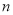 个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为
个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为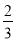 ,则
,则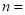 .
.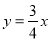 与双曲线
与双曲线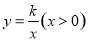 交于点A。将直线
交于点A。将直线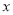 轴交于点C,若
轴交于点C,若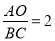 ,则
,则 的值为( )
的值为( )