题目内容
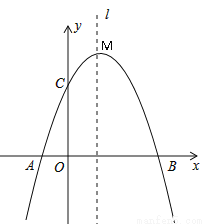
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
题目内容
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案