Question

如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．

（1）求证：PQ∥AB；（2）若点D在∠BAC的平分线上，求CP的长；

 

Answer 1

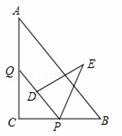
解：（1）证明：∵在Rt△ABC中，AB=15，BC=9，∴．

∵，∴．又∵∠C=∠C，∴△PQC∽△BAC.∴∠CPQ=∠B. ∴PQ∥AB.

（2）如答图1，连接AD，∵PQ∥AB，∴∠ADQ=∠DAB．∵点D在∠BAC的平分线上，∴∠DAQ=∠DAB.∴∠ADQ=∠DAQ. ∴AQ=DQ．在Rt△CPQ中，∵CP=3x，CQ=4x，∴PQ=5x.∵PD=PC=3x，∴DQ=2x．∵AQ=12﹣4x，∴12﹣4x=2x，解得x=2.∴CP=3x=6．