题目内容
 如图,∠ACB=∠BDC=90°,BD=4,BC=5,则AC=
如图,∠ACB=∠BDC=90°,BD=4,BC=5,则AC=考点:相似三角形的判定
专题:常规题型
分析:先根据勾股定理得到CD=3,再根据相似三角形的判定方法,当AC:BD=BC:CD时,△ACB∽△BDC,则AC:4=5:3,然后根据比例性质求解.
解答:解:在Rt△BDC中,∵BD=4,BC=5,
∴CD=
=3,
∵∠ACB=∠BDC=90°,
∴当AC:BD=BC:CD时,△ACB∽△BDC,
即AC:4=5:3,
∴AC=
,
即AC=
时,△ACB∽△BDC.
故答案为
.
∴CD=
| BC2-BD2 |
∵∠ACB=∠BDC=90°,
∴当AC:BD=BC:CD时,△ACB∽△BDC,
即AC:4=5:3,
∴AC=
| 20 |
| 3 |
即AC=
| 20 |
| 3 |
故答案为
| 20 |
| 3 |
点评:本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了勾股定理.

练习册系列答案
相关题目
下列说法正确的是( )
| A、0既不是整数也不是分数 |
| B、互为相反数的两个数的绝对值相等 |
| C、一个数的绝对值一定是正数 |
| D、绝对值等于本身的数是0和1 |
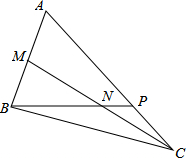 已知:M是AB的中点,AP=2PC,BP=4,求PN的长.
已知:M是AB的中点,AP=2PC,BP=4,求PN的长.