题目内容
6、若关于未知数x的方程x2+(m+2)x+m+5=0的两根都是正数,则m的取值范围是
-5<m≤-4
.分析:先设方程x2+(m+2)x+m+5=0的两根为α,β,则α+β=-(m+2),αβ=m+5,根据题意列出不等式,求出m的取值范围即可.
解答:解:设方程x2+(m+2)x+m+5=0的两根为α,β,
∴△≥0,α+β=-(m+2),αβ=m+5,
∵α>0,β>0,
∴-(m+2)>0,m+5>0,
m<-2且m>-5,
∵△≥0,
∴(m+2)2-4(m+5)≥0,
解得m≥4,m≤-4,
∴m的取值范围是-5<m≤-4.
故答案为:-5<m≤-4.
∴△≥0,α+β=-(m+2),αβ=m+5,
∵α>0,β>0,
∴-(m+2)>0,m+5>0,
m<-2且m>-5,
∵△≥0,
∴(m+2)2-4(m+5)≥0,
解得m≥4,m≤-4,
∴m的取值范围是-5<m≤-4.
故答案为:-5<m≤-4.
点评:本题考查了一元二次方程根与系数的关系,方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-$frac{b}{a}$,x1•x2=$frac{c}{a}$.

练习册系列答案
相关题目
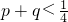 .
.