题目内容
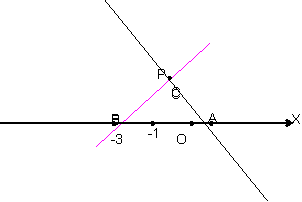
在平面直角坐标系中,点O是原点。直线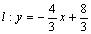 与x轴交于点A,过点B(-3,0)作BC⊥l,垂足为C,点D是直线BC上的一个动点;
与x轴交于点A,过点B(-3,0)作BC⊥l,垂足为C,点D是直线BC上的一个动点;
(1)求直线与y轴的交点P的坐标和线段BC的长度
(2)若CD=1,求点D的坐标;
‚过点D做直线m∥l,交x轴于点E,连接CE,,当点D在线段CB上运动时,求出使得三角形CDE的面积最大时点D的位置;
ƒ在直线C
|
 存在点
存在点 D使三角形CDE的面积等于
D使三角形CDE的面积等于
|
 | |||
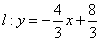 | |||
(1) 令x=0,则y= ∴直线与y轴的交点P(0,
∴直线与y轴的交点P(0, )
)
(2) 求线段BC的方法有:
方法一:由题易知△ABC~△APO ∴ BC=4
方法二:由题知

∵AB=5 ∴BC=4
(2) 分类讨论:
若点D在点C左边,则BD1=3,利用三角函数或相似解得
若点D在点C右边,则BD2=5,利用三角函数 或相似解得……3分(对一个得2分)
或相似解得……3分(对一个得2分)




‚:参考的做法,设CD=a,则BD=4-a,
∵m∥l,BC⊥l
∴BC⊥m
∴△BDE是RT△
 利用三角函数或者相似可得:DE=
利用三角函数或者相似可得:DE=
∴
|

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
如图1,矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
|
|
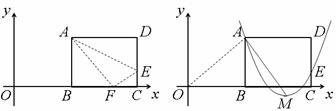
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图2,设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连结AM,
若∠OAM=90°,求a、h、m的值.

 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为_______________,请简单说明理由。
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为_______________,请简单说明理由。 肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )
肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )
 的内部,
的内部, ,则圆O的半径为( )
,则圆O的半径为( ) B.
B. C.
C. D.
D.

 )
) (
( )的
)的 小,这个运算符号是( )
小,这个运算符号是( )