题目内容
4.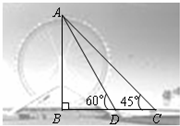 2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.
2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.
分析 设AB=xm,则BC=xm,BD=(x-50)m,然后在Rt△ABD中,利用三角函数解答.
解答 解:设AB=xm,则BC=xm,BD=(x-50)m,
在Rt△ABD中,tan60°=$\frac{AB}{BD}$=$\frac{x}{x-50}$=$\sqrt{3}$,
解得:x=25($\sqrt{3}$+3)m,
答:摩天轮高度为25($\sqrt{3}$+3)m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,构造三角函数数学模型是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.计算5a-a结果正确的是( )
| A. | 4a | B. | 5 | C. | -4 | D. | -4a |
19.比1小3的数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | 1 |
9.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (a2)3=a5 | C. | 2a2-a2=2 | D. | a5•a2=a7 |
16. 如图,在△ABC中,∠B=85°,∠ACB=45°,若CD∥AB,则∠ACD的度数为( )
如图,在△ABC中,∠B=85°,∠ACB=45°,若CD∥AB,则∠ACD的度数为( )
 如图,在△ABC中,∠B=85°,∠ACB=45°,若CD∥AB,则∠ACD的度数为( )
如图,在△ABC中,∠B=85°,∠ACB=45°,若CD∥AB,则∠ACD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |
13. 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | $\frac{π}{6}$ | C. | 4$\sqrt{3}$-$\frac{2π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
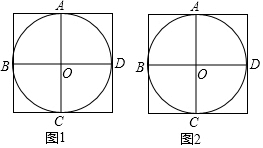 在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.
在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P.