题目内容
11. 如图,正方形ABCD中,E是BC中点,AE与BD相交于F,求证:CF⊥DE.
如图,正方形ABCD中,E是BC中点,AE与BD相交于F,求证:CF⊥DE.
分析 如图,利用正方形的性质得BA=BC=CD,∠ABF=∠CBF=45°,则可根据“SAS”证明△ABF≌△CBF,得到∠1=∠2,再证明△ABE≌△DCE得到∠1=∠3,则∠2=∠3,由于∠2+∠4=90°,则∠3+∠4=90°,于是可判断CF⊥DE.
解答 证明:如图,
∵四边形ABCD为正方形,
∴BA=BC=CD,∠ABF=∠CBF=45°,
在△ABF和△CBF中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
∴△ABF≌△CBF,
∴∠1=∠2,
∵E点为BC的中点,
∴BE=CE,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠ABE=∠DCE}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE,
∴∠1=∠3,
∴∠2=∠3,
而∠2+∠4=90°,
∴∠3+∠4=90°,
∴∠DGC=90°,
∴CF⊥DE.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
19.2015年春我国大部分地区出现严重雾霾,为了增强同学们的环保意识,某校组织了一次防治雾霾知识竞赛,两组学生成绩统计如下:
已知算得两个组的人均分数都是80分,请根据你所学过的统计知识,进一步判断这两个组这次成绩谁优谁次,并说明理由.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
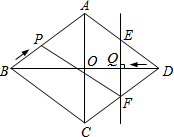 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
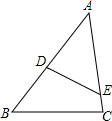 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.