题目内容
1.解方程组:$\left\{\begin{array}{l}{3y-5z=0}\\{5x-4y=0}\\{2x-y+z=6}\end{array}\right.$.分析 先消去方程组中的z,再根据二元一次方程组的解法解答即可.
解答 解:$\left\{\begin{array}{l}{3y-5z=0①}\\{5x-4y=0②}\\{2x-y+z=6③}\end{array}\right.$,
①+③×5得:10x-2y=30④,
联立方程组得:$\left\{\begin{array}{l}{5x-4y=0②}\\{10x-2y=30④}\end{array}\right.$,
④×2-②得:15x=60,
解得:x=4,
把x=4代入②得:y=5,
把y=5代入①得:z=3,
所以方程组的解是:$\left\{\begin{array}{l}{x=4}\\{y=5}\\{z=3}\end{array}\right.$.
点评 解三元一次方程组要注意以下几点:
方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,⊙O的弦AB、CD交于点P,连接AC、BD,求证:△BDP∽△CAP.
如图所示,⊙O的弦AB、CD交于点P,连接AC、BD,求证:△BDP∽△CAP. 如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).
如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).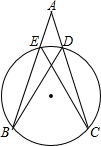 如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.
如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.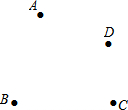 作图题.如图,在同一平面内有四个点A、B、C、D,
作图题.如图,在同一平面内有四个点A、B、C、D,