题目内容
 如图,A、B是⊙O上两点,且∠AOB=70°,C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是________.
如图,A、B是⊙O上两点,且∠AOB=70°,C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是________.
35°或145°
分析:此题应分两种情况:
①当点C在优弧AB上时,根据圆周角定理可知∠ACB= ∠AOB;
∠AOB;
②当点C在劣弧AB上时,根据圆内接四边形的性质可求出此时∠ACB的度数.
解答: 解:如图:
解:如图:
∵∠AOB=70°,
∴∠ACB= ∠AOB=35°;
∠AOB=35°;
∵四边形ACBC′内接于⊙O,
∴∠AC′B=180°-∠ACB=145°;
当C在优弧AB上时,∠ACB=35°,
当C在劣弧AB上时,∠ACB=145°;
故∠ACB的度数为35°或145°.
点评:此题主要考查的是圆周角定理和圆内接四边形的性质,应考虑到∠ACB的度数有两种情况,不要漏解.
分析:此题应分两种情况:
①当点C在优弧AB上时,根据圆周角定理可知∠ACB=
 ∠AOB;
∠AOB;②当点C在劣弧AB上时,根据圆内接四边形的性质可求出此时∠ACB的度数.
解答:
 解:如图:
解:如图:∵∠AOB=70°,
∴∠ACB=
 ∠AOB=35°;
∠AOB=35°;∵四边形ACBC′内接于⊙O,
∴∠AC′B=180°-∠ACB=145°;
当C在优弧AB上时,∠ACB=35°,
当C在劣弧AB上时,∠ACB=145°;
故∠ACB的度数为35°或145°.
点评:此题主要考查的是圆周角定理和圆内接四边形的性质,应考虑到∠ACB的度数有两种情况,不要漏解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )| A、65° | B、35° | C、70° | D、55° |
 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.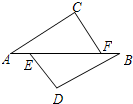 已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;
已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;