题目内容
1.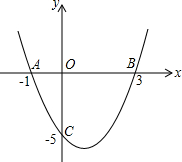 如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),
如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),(1)试确定此二次函数的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使PB+PC的值最小?如果存在,请求出点P的坐标;如果不存在,请说明理由.
分析 (1)根据题意设二次函数的解析式为y=a(x+1)(x-3),代入C(0,-5)求得a的值即可;
(2)先求得对称轴为直线x=1,然后利用待定系数法确定直线BC的关系式为y=$\frac{5}{3}$x-5,由于使得PB+PC的值最小的点P为直线BC与对称轴的交点,把x=1代入为y=$\frac{5}{3}$x-5即可确定P点坐标.
解答  解:(1)根据题意设二次函数的解析式为y=a(x+1)(x-3),
解:(1)根据题意设二次函数的解析式为y=a(x+1)(x-3),
代入C(0,-5)得,-5=-3a,
解得a=$\frac{5}{3}$.
故二次函数的解析式为y=$\frac{5}{3}$(x+1)(x-3)=$\frac{5}{3}$x2-$\frac{10}{3}$x-5;
(2)作抛物线的对称轴l,交BC于P,
∵抛物线的对称轴x=-$\frac{b}{2a}$=1,
∴P点的横坐标为1,.
设直线BC的函数表达式为y=kx+t(k≠0).
∵由B(3,0),C(0,-5),
∴$\left\{\begin{array}{l}{3k+t=0}\\{t=-5}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=\frac{5}{3}}\\{t=-5}\end{array}\right.$.
∴直线BC的函数表达式为y=$\frac{5}{3}$x-5.
将x=1代入得y=-$\frac{10}{3}$.
∴P点的坐标为(1,-$\frac{10}{3}$).
点评 本题综合考查了待定系数法求函数解析式、轴对称-最短路线问题,(2)题的关键点是确定点P的位置.

练习册系列答案
相关题目
11.如下书写的四个汉字,其中为轴对称图形的是( )
| A. | 上 | B. | 善 | C. | 若 | D. | 水 |
16.将一元二次方程x2-2x-2=0配方后所得的方程是( )
| A. | (x-2)2=2 | B. | (x-1)2=2 | C. | (x-1)2=3 | D. | (x-2)2=3 |
6.小明的座位在第5排第4列,简记为(5,4),张扬的座位在第3排第2列,简记为(3,2),若小伟的座位在小明的后面相距2排,同时在他的左边相距3列,则小伟的座位可简记为( )
| A. | (2,7) | B. | (7,1) | C. | (8,2) | D. | (6,5) |
 电子钟镜子里的像如图所示,实际时间是10:51.
电子钟镜子里的像如图所示,实际时间是10:51.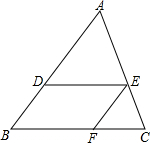 如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.
如图,在三角形ABC中,DE∥BC,EF∥AB,AD:DB=3:2,BC=25,求FC的长.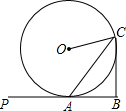 如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.
如图,AB为⊙O的切线,A为切点,点C在⊙O上,BC⊥PB于点 B,OC为⊙O的半径.