题目内容
3.如图,等腰三角形ABC,∠ABC=90°,AB=AC,E在AB上,D是CE延长线上一点,AD=AE.(1)如图1,若∠BCD:∠BCA=1:3,求证:CD=AC.
(2)在(1)条件下,如图2,延长AD,CB交于点F,试猜想DF,BF与BC之间的数量关系,并证明你的猜想.
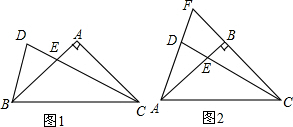
分析 (1)根据等腰直角三角形的性质得∠BCA=45°,则由∠BCD:∠BCA=1:3可计算出∠BCD=15°,所以∠ACD=30°,∠BEC=75°,利用对顶角相等得∠AED=∠BEC=75°,由于AD=AE,则∠ADE=∠AED=75°,接着利用三角形内角和计算出∠DAC=75°,则∠ADC=∠DAC,然后根据等腰三角形的判定即可得到CD=CA;
(2)如图2,先计算出∠DAB=30°,然后在Rt△ABF中利用正切定义得到tan∠FAB=tan30°=$\frac{BF}{AB}$=$\frac{\sqrt{3}}{3}$,加上AB=CB,于是得到BF=$\frac{\sqrt{3}}{3}$BC.
解答 (1)证明: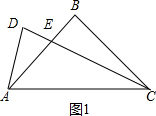 ∵∠ABC=90°,AB=CB,
∵∠ABC=90°,AB=CB,
∴∠BCA=45°,
∵∠BCD:∠BCA=1:3,
∴∠BCD=15°,
∴∠ACD=45°-15°=30°,∠BEC=90°-15°=75°,
∴∠AED=∠BEC=75°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∵∠DAC=180°-∠ADE-∠ACD=75°,
∴∠ADC=∠DAC,
∴CD=CA;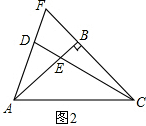 (2)解:BF=$\frac{\sqrt{3}}{3}$BC.理由如下:如图2,
(2)解:BF=$\frac{\sqrt{3}}{3}$BC.理由如下:如图2,
∵∠DAC=75°,
∴∠DAB=75°-45°=30°,
∵∠ABF=90°,
在Rt△ABF中,tan∠FAB=tan30°=$\frac{BF}{AB}$=$\frac{\sqrt{3}}{3}$,
∵AB=CB,
∴BF=$\frac{\sqrt{3}}{3}$BC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形;在应用全等三角形的性质时主要是得到对应角相等或对应线段相等.解决本题的关键是灵活应用等腰直角三角形的性质.

| A. | (a2)3=a8 | B. | a8÷a4=a2 | C. | a3+a2=a5 | D. | a2•a3=a5 |
| A. | 任意掷一枚均匀的硬币,正面朝上 | B. | 篮球运动员投篮,投进篮筐 | ||
| C. | 一个星期有七天 | D. | 打开电视机,正在播放新闻 |
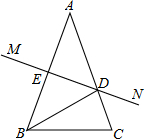 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°. 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点. 如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.
如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.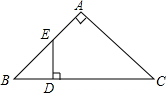 如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.
如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.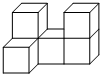 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )
如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )