题目内容
已知△ABC与△DEF相似，相似比为2：3，△ABC的周长是10cm，△DEF的周长是（ ）
| A、10cm | B、15cm |
| C、20cm | D、30cm |
考点：相似三角形的性质
专题：
分析：由△ABC与△DEF相似，相似比为2：3，可求得其周长比为：2：3，然后由△ABC的周长是10cm，求得△DEF的周长．
解答：解：∵△ABC与△DEF相似，相似比为2：3，
∴周长比为：2：3，
∵△ABC的周长是10cm，
∴△DEF的周长是15cm．
故选B．
∴周长比为：2：3，
∵△ABC的周长是10cm，
∴△DEF的周长是15cm．
故选B．
点评：此题考查了相似三角形的性质．此题比较简单，注意相似多边形的周长比等于相似比．
练习册系列答案
阅读快车系列答案
相关题目
下列说法错误的是（ ）
| A、两个互余的角都是锐角 |
| B、锐角的补角大于这个角本身 |
| C、互为补角的两个角不可能都是锐角 |
| D、锐角大于它的余角 |
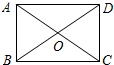如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=2，则矩形的边长BC的长是（ ）| A、2 | ||
| B、4 | ||
C、2
| ||
D、4
|
若方程2x3-5m+5（m-1）=0是关于x的一元一次方程，则这个方程的解是（ ）
A、
| ||
B、-
| ||
C、
| ||
| D、3 |
如图，在平面直角坐标系中，点A，B的坐标分别为（-6，0），（0，8），以点A为圆心，以AB长为半径画弧，交x轴正半轴于点C，则点C的坐标为（ ）| A、（10，0） |
| B、（0，4） |
| C、（4，0） |
| D、（2，0） |
△ABC中，∠A，∠B，∠C的对边分别为a，b，c，由下列条件不能判定△ABC为直角三角形的是（ ）
| A、∠A+∠B=∠C |
| B、a：b：c=3：4：6 |
| C、a2=c2-b2 |
| D、a=7，b=24，c=25 |
