题目内容
【题目】在矩形
中，将点
翻折到对角线
上的点
处，折痕
交
于点
．将点
翻折到对角线上的点
处，折痕
交
于点
．
求证：四边形
为平行四边形；
若四边形为菱形，且
，求的长．
【答案】（1）见解析；（2）
．
【解析】
（1）证△ABE≌△CDF，推出AE=CF，求出DE=BF，DE∥BF，根据平行四边形判定推出即可．
（2）求出∠ABE=30°，根据直角三角形性质求出AE、BE，即可求出答案．
解：
证明：∵四边形
是矩形，
∴
，
，
，
∴
，
由折叠的性质可得：
，
，
∴
，
在
和
中
，
∴
，
∴
，
∵四边形是矩形，
∴
，
，
∴
，
，
∴四边形
为平行四边形；
解法二：证明：∵四边形是矩形，
∴，，，
∴，
∴
，
∴
，
∵
，
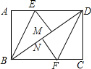
∴四边形为平行四边形．
解：∵四边形为菱形，
∴
，
，
∵四边形是矩形，
∴，
，
∴
，
∵
，
，
∴
，
，
∴
．
练习册系列答案
相关题目
