题目内容
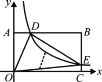
【题目】如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数
(x＞0)与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9,则k的值是( )
A.
B.
C.
D.12
【答案】C
【解析】
设B点的坐标为（a，b），由BD=3AD，得D（
，b），根据反比例函数定义求出关键点坐标，根据S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE= 9求出k.
∵四边形OCBA是矩形，
∴AB=OC，OA=BC，
设B点的坐标为（a，b），
∵BD=3AD，
∴D（，b），
∵点D，E在反比例函数的图象上，
∴
=k，
∴E（a，
），
∵S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE=ab-
--
（b-）=9，
∴k=
，
故选：C
练习册系列答案
一线名师权威作业本系列答案
相关题目
