题目内容
9.⊙O是△ABC的外接圆,AB是直径,过$\widehat{BC}$的中点P作⊙O的直径PG交弦$\widehat{BC}$于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求tan∠BAC的值;
(2)如图2,在DG上取一点K,使DK=DP,连接CK,若KG=2,KP=6,求CK的长.
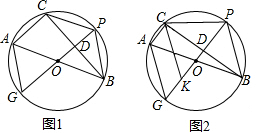
分析 (1)如图1,根据垂径定理得到PG⊥BC,则BD垂直平分OP,于是可判断△OBP为等边三角形,所以∠BOP=60°,然后估计圆周角定理得到∠BAC=∠BOP=60°;
(2)由垂径定理得到PD⊥BC,CD=BD,根据勾股定理得到BD=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$,CD=$\sqrt{15}$,再根据勾股定理即可得到结论.
解答 解:(1)∵AB为⊙O直径,点P是$\widehat{BC}$的中点,
∴PG⊥BC,即∠ODB=90°.
∵D为OP的中点,
∴BD垂直平分OP,
∴BP=BO,
而OB=OP,
∴△OBP为等边三角形,
∴∠BOP=60°,
∴∠BAC=∠BOP=60°,
∴tan∠BAC=$\sqrt{3}$;
(2)∵点P是$\widehat{BC}$的中点,
∴PD⊥BC,CD=BD,
∵KG=2,KP=6,
∴OB=OP=4,
∴DK=DP=3,
∴OD=1,
∴BD=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$,
∴CD=$\sqrt{15}$,
∴CK=$\sqrt{C{D}^{2}+D{K}^{2}}$=$\sqrt{(\sqrt{15})^{2}+{3}^{2}}$=2$\sqrt{6}$.
点评 本题考查了垂径定理,解直角三角形,等边三角形的判定和性质,准确的理解题意是解题的关键.

练习册系列答案
相关题目
4.已知点A(2,-2),B(-1,-2),则直线AB与x轴的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 相互垂直 | D. | 不能确定 |
14. 一个物体的三视图如下图所示,则该物体是( )
一个物体的三视图如下图所示,则该物体是( )
 一个物体的三视图如下图所示,则该物体是( )
一个物体的三视图如下图所示,则该物体是( )| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 长方体 |
1.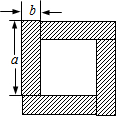 如图,4块安全相同的长方形围成一个正方形,图中阴影部分的面积可以用不同的代数式进行表示,由此能验证的式子是( )
如图,4块安全相同的长方形围成一个正方形,图中阴影部分的面积可以用不同的代数式进行表示,由此能验证的式子是( )
 如图,4块安全相同的长方形围成一个正方形,图中阴影部分的面积可以用不同的代数式进行表示,由此能验证的式子是( )
如图,4块安全相同的长方形围成一个正方形,图中阴影部分的面积可以用不同的代数式进行表示,由此能验证的式子是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2-(a-b)2=2ab | C. | (a+b)2-(a-b)2=4ab | D. | (a-b)2+2ab=a2+b2 |
19.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | a6÷a=a5 | C. | x3•x4=x12 | D. | ${(\sqrt{3}+2)}^{2}$=7 |
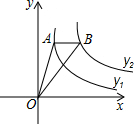 如图,反比例函数y1=$\frac{k}{x}$(0<k<3,x>0)与y2=$\frac{3}{x}$(x>0)的图象如图所示,反比例函数y1的图象上有一点A,其横坐标为a,过点A作x轴的平行线交反比例函数y2的图象于点B,连接AO、BO,若△ABO的面积为S,则S关于a的大致函数图象是( )
如图,反比例函数y1=$\frac{k}{x}$(0<k<3,x>0)与y2=$\frac{3}{x}$(x>0)的图象如图所示,反比例函数y1的图象上有一点A,其横坐标为a,过点A作x轴的平行线交反比例函数y2的图象于点B,连接AO、BO,若△ABO的面积为S,则S关于a的大致函数图象是( )
 如图,小丽从A点出发前进6m,向右转40°,再前进6m,又右转40°,…,这样一直走下去,当她第一次回到出发点A时,一共走了54m.
如图,小丽从A点出发前进6m,向右转40°,再前进6m,又右转40°,…,这样一直走下去,当她第一次回到出发点A时,一共走了54m.