Question

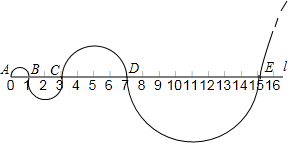
如图，在标有刻度的直线l上，从点A开始，
以AB=1为直径画半圆，记为第1个半圆；
以BC=2为直径画半圆，记为第2个半圆；
以CD=4为直径画半圆，记为第3个半圆；
以DE=8为直径画半圆，记为第4个半圆，
…按此规律，继续画半圆，则第4个半圆的面积是第3个半圆面积的    倍，第n个半圆的面积为    （结果保留π）

Answer 1

【答案】分析：根据已知图形得出第4个半圆的半径和第3个半圆的半径，进而得出第4个半圆的面积与第3个半圆面积的关系，得出第n个半圆的半径，进而得出答案．
解答：解：∵以AB=1为直径画半圆，记为第1个半圆；
以BC=2为直径画半圆，记为第2个半圆；
以CD=4为直径画半圆，记为第3个半圆；
以DE=8为直径画半圆，记为第4个半圆，
∴第4个半圆的面积为：=8π，
第3个半圆面积为：=2π，
∴第4个半圆的面积是第3个半圆面积的=4倍；
根据已知可得出第n个半圆的直径为：2^n-1，
则第n个半圆的半径为：=2^n-2，
第n个半圆的面积为：=2^2n-5π．
故答案为：4，2^2n-5π．
点评：此题主要考查了数字变化规律，注意数字之间变化规律，根据已知得出第n个半圆的直径为：2^n-1是解题关键．