题目内容
 (2012•广州)如图,在标有刻度的直线l上,从点A开始,
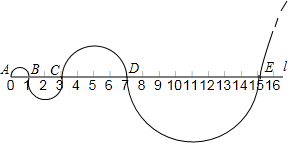
(2012•广州)如图,在标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
…按此规律,继续画半圆,则第4个半圆的面积是第3个半圆面积的
4
4
倍,第n个半圆的面积为22n-5π
22n-5π
(结果保留π)分析:根据已知图形得出第4个半圆的半径和第3个半圆的半径,进而得出第4个半圆的面积与第3个半圆面积的关系,得出第n个半圆的半径,进而得出答案.
解答:解:∵以AB=1为直径画半圆,记为第1个半圆;
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
∴第4个半圆的面积为:
=8π,
第3个半圆面积为:
=2π,
∴第4个半圆的面积是第3个半圆面积的
=4倍;
根据已知可得出第n个半圆的直径为:2n-1,
则第n个半圆的半径为:
=2n-2,
第n个半圆的面积为:
=22n-5π.
故答案为:4,22n-5π.
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
∴第4个半圆的面积为:
| π×42 |
| 2 |
第3个半圆面积为:
| π×22 |
| 2 |
∴第4个半圆的面积是第3个半圆面积的
| 8π |
| 2π |
根据已知可得出第n个半圆的直径为:2n-1,
则第n个半圆的半径为:
| 2 n-1 |
| 2 |
第n个半圆的面积为:
| π× (2n-2) 2 |
| 2 |
故答案为:4,22n-5π.
点评:此题主要考查了数字变化规律,注意数字之间变化规律,根据已知得出第n个半圆的直径为:2n-1是解题关键.

练习册系列答案
相关题目
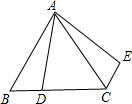 (2012•广州)如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为
(2012•广州)如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )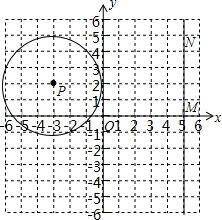 (2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(2012•广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.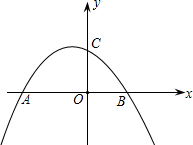 (2012•广州)如图,抛物线y=
(2012•广州)如图,抛物线y=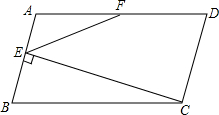 (2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).