Question

【题目】实验探究：下面设想用电脑模拟台球游戏，为简单起见，约定：①每个球或球袋都视为一点，如不遇障碍，各球均沿直线前进；②A球击中B球，意味着B球在A球前进的路线上，且B球被撞击后沿着A球原来的方向前进；③球撞及桌边后的反弹角等于入射角（即∠α＝∠β）．如图，设桌面上只剩下白球A和6号球B，希望A球撞击桌边上C点后反弹，再击中B球．

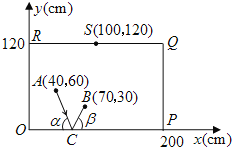
（1）在桌面上建立如图所示的坐标系，白球A（40，60）和6号球B（70，30），利用一次函数的知识，求出C点坐标；

（2）设桌边RQ上有球袋S（100，120），判定6号球被从C点反弹出的白球撞击后，能否落入球袋S中（假定6号球被撞击后的速度足够大），并说明理由．

Answer 1

【答案】（1）点C的坐标为（60，0）；（2）能落入球袋S中，理由见解析；

【解析】

（1）作点A关于x轴的对称点A′，利用待定系数法求出直线A′B的解析式，即可得到点C的坐标；

（2）把点S的坐标代入直线A′B的解析式，判断即可．

解：（1）作点A关于x轴的对称点A′，连接A′B，则A′、C、B在同一条直线上，

∵点A′是点A关于x轴的对称点，A（40，60），

∴点A′的坐标为（40，﹣60），

设直线A′B的解析式为y＝kx+b，

则，

解得，，

∴直线A′B的解析式为y＝3x﹣180，

当y＝0时，x＝60，

∴点C的坐标为（60，0）；

（2）能落入球袋S中，

理由：把x＝100代入直线A′B的解析式得，y＝3×100﹣180＝120，

∴S（100，120）在直线A′B上，

∴能落入球袋S中．