题目内容
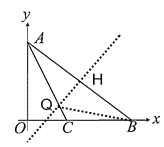
【题目】如图,在![]() 中,
中,![]() 是原点,
是原点,![]() (0,3),
(0,3),![]() (4,0),
(4,0),![]() 是
是![]() 的角平分线.
的角平分线.

(1)确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出点
轴的距离相等,若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)在线段![]() 上是否有一点
上是否有一点![]() ,使
,使![]() 是等腰三角形,若存在,直接写出 点
是等腰三角形,若存在,直接写出 点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)直线AB的解析式为:![]() ;(2)点
;(2)点![]() 的坐标为(1,1);(3)点Q的坐标为:(
的坐标为(1,1);(3)点Q的坐标为:(![]() ,
,![]() ).
).
【解析】
(1)直接利用待定系数法求解即可;
(2)过点C作CE⊥AB,设OC=CE=x,则BC=4-x,求出BE=2,然后在Rt△BCE中,利用勾股定理构建方程求出OC得到C点坐标,求出直线AC的解析式,联立直线AC的解析式和y=x,求出交点坐标即可;
(3)作线段AB的垂直平分线QH交AC于Q,交AB与H,设出直线QH的解析式,求出点H的坐标,代入可得直线QH的解析式,联立直线QH与直线AC的解析式,求出交点坐标即可.
解:(1)设直线AB的解析式为:y=kx+b,
代入A(0,3),B(4,0)得:![]() ,
,
解得: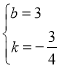 ,
,
∴直线AB的解析式为:![]() ;
;
(2)过点C作CE⊥AB,
∵AC平分∠OAB,
∴OC=CE,
∴设OC=CE=x,则BC=4-x,
易证△AOC≌△ACE,则AE=OA=3,
∵AB![]() ,
,
∴BE=5-3=2,
在Rt△BCE中,CE2+BE2=BC2,即x2+22=(4-x)2,
解得:![]() ,
,
∴C(![]() ,0),
,0),
设直线AC的解析式为:y=mx+n,
代入A(0,3),C(![]() ,0)得:
,0)得: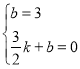 ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=-2x+3,
∵点![]() 在线段
在线段![]() 上,且到
上,且到![]() 轴和
轴和![]() 轴的距离相等,
轴的距离相等,
∴点P在直线y=x上,
联立![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为(1,1);
的坐标为(1,1);
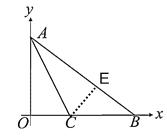
(3)∵点Q在线段AC上,△AQB是等腰三角形,
∴如果存在,只有AQ=BQ一种情况,
作线段AB的垂直平分线QH交AC于Q,交AB与H,
∵直线AB的解析式为:![]() ,
,
∴ 设直线QH的解析式为:![]() ,
,
∵A(0,3),B(4,0),
∴H(2,![]() ),
),
将点H(2,![]() )代入
)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴直线QH的解析式为:![]() ,
,
联立直线QH与直线AC解析式得: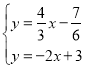 ,
,
解得:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ).
).