题目内容

已知
-ax+y=b
cx+y=d
的解为
x=1
y=2
，则直线y=ax+b与y=-cx+d的交点坐标为（　　）
A、（1，2）
B、（-1，2）
C、（1，-2）
D、（-1，-2）
分析：将方程组的两个方程变形可得直线y=ax+b与y=-cx+d，故“直线y=ax+b与y=-cx+d的交点坐标为（　　）”转化为“方程组
-ax+y=b
cx+y=d
的解为（　　）”的问题，由题意可知，方程组
-ax+y=b
cx+y=d
的解就是本题的答案．
解答：解：∵直线y=ax+b与y=-cx+d的交点坐标就是方程组
y=ax+b
y=-cx+d
的解，
∴由该方程组得：
-ax+y=b
cx+y=d
，
又∵方程组
-ax+y=b
cx+y=d
的解为
x=1
y=2
，
∴方程组
y=ax+b
y=-cx+d
的解为
x=1
y=2
，
∴直线y=ax+b与y=-cx+d的交点坐标为（1，2）；
故选A．
点评：解答本题的关键是正确理解“直线y=ax+b与y=-cx+d的交点坐标”就是方程组
y=ax+b
y=-cx+d
的解．
练习册系列答案
相关题目
已知一次函数y=ax+b的图象经过点A（
3
，
3
+2），B（-1，
3
），C（c，2-c）．求a2+b2+c2-ab-bc-ca的值．
已知抛物线y=x2-（a+b）x+
c2
4
，其中a、b、c分别为△ABC中∠A，∠B，∠C的对边．
（1）求证：该抛物线与x轴必有两个不同的交点；
（2）设抛物线与x轴的两个交点为P、Q，顶点为R，且∠PQR=α，tanα=
5
，若△ABC的周长为10，求抛物线的解析式；
（3）设直线y=ax-bc与抛物线y=x2-（a+b）x+
c2
4
交于点E、F，与y轴交于点M，且抛物线对称轴为x=a，O是坐标原点，△MOE与△MOF的面积之比为5：1，试判断△ABC的形状并证明你的结论．
已知四个互不相等的实数x1，x2，x3，x4，其中x1＜x2，x3＜x4．
（1）请列举x1，x2，x3，x4从小到大排列的所有可能情况；
（2）已知a为实数，函数y=x2-4x+a与x轴交于（x1，0），（x2，0）两点，函数y=x2+ax-4与x轴交于（x3，0），（x4，0）两点．若这四个交点从左到右依次标为A，B，C，D，且AB=BC=CD，求a的值．
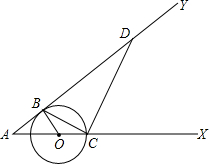（2012•龙湾区二模）如图，已知O是射线AX上的一点，以点O为圆心、r为半径的圆与射线AY切于点B，交射线OX于点C．连接BC，作CD⊥BC，交射线AY于点D．
（1）求证：△ABC∽△ACD；
（2）若r=6，sinA=
35
，求AD的值．
已知：△ABC中，AX，BY，CZ分别是BC，AC，AB边上的中线，求证：AX，BY，CZ相交于一点G，并且AG：GX=2：1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网