Question

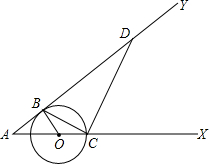（2012•龙湾区二模）如图，已知O是射线AX上的一点，以点O为圆心、r为半径的圆与射线AY切于点B，交射线OX于点C．连接BC，作CD⊥BC，交射线AY于点D．
（1）求证：△ABC∽△ACD；
（2）若r=6，sinA=

3

5

，求AD的值．

Answer 1

分析：（1）根据切线的定义可得BO⊥AD，然后求出∠ABO=∠BCD，再根据等边对等角的性质可得∠OBC=∠OCB，然后求出∠ABC=∠ACD，再利用两角对应相等，两三角形相似证明即可；
（2）根据∠A的正弦值先求出OA，然后求出AC，再利用勾股定理列式求出AB，然后根据相似三角形对应边成比例列式计算即可得解．

解答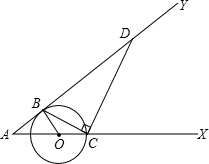：（1）证明：∵⊙O与射线AY切于点B，
∴BO⊥AD，
∵CD⊥BC，
∴∠ABO=∠BCD=90°，
∵OB=OC，
∴∠OBC=∠OCB，
∴∠ABC=∠ACD，
又∵∠A=∠A，
∴△ABC∽△ACD；

（2）∵BO⊥AD，r=6，sinA=

3

5

，
∴AO=10，
∴AC=AO+OC=10+6=16，
AB=

AO2-BO2

=

102-62

=8，
∵△ABC∽△ACD，
∴

AC

AD

=

AB

AC

，
∴

16

AD

=

8

16

，
解得AD=32．

点评：本题是圆的综合题，主要利用了相似三角形的判定与性质，圆的切线的定义，勾股定理的应用，根据圆的半径相等、利用等边对等角找出三角形相似的条件是解题的关键，也是本题的突破口．