题目内容
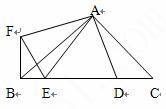
如图,在RtΔABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45º,将ΔADC绕点A顺时针旋转90º后,得到ΔAFB,连结EF.则∠EAF=____.
45º

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
题目内容
如图,在RtΔABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45º,将ΔADC绕点A顺时针旋转90º后,得到ΔAFB,连结EF.则∠EAF=____.

45º

 小学期末标准试卷系列答案
小学期末标准试卷系列答案