题目内容
探究:如图①,在矩形ABCD中,过点A作∠EAF=∠BAD,AE交线段BC于点E,AF交线段CD的延长线于点F.求证:ΔABE∽ΔADF.
拓展:如图②,在四边形ABCD中,∠ABC+∠ADF=180º,过点A作∠EAF=∠BAD,AE交线段BC于点E,AF交线段CD延长线于点F.若AB∶AD=2∶3,求ΔABE的面积与ΔADF的面积之比.

探究:证明:∵在矩形ABCD中 ∴∠ADC=∠BAD=∠B=90º
∴∠ADF=∠B=90º, ∵∠EAF=∠BAD,
∴∠EAB+∠EAD=∠FAD+∠EAD, ∴∠EAB=∠FAD
∴ΔABE∽ΔADF
拓展:解:∵∠ABC+∠ADC=180º, ∠ADC+ADF=180º.
∴∠ABE=∠ADF, ∵∠EAF=∠BAD,
∴∠EAB+∠EAD=∠FAD+∠EAD, ∴∠EAB=∠FAD
∴ΔABE∽ΔADF. ∴SΔABE∶SΔADF=AB2∶AD2=4∶9

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,组成一个五位数x,把b放在a的左边,组成一个五位数y,试问9能否整除x-y?请说明理由。
,组成一个五位数x,把b放在a的左边,组成一个五位数y,试问9能否整除x-y?请说明理由。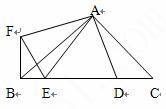

 应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( ) (B) 4,1,6,7
(B) 4,1,6,7
 B.
B.
 D.
D.

