题目内容
5.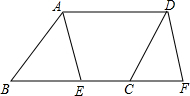 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠AEB=∠DFC.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠AEB=∠DFC.
分析 根据平行四边形的性质可得AB=CD,AD=BC,AB∥CD,进而可得∠ABE=∠DCF,利用SAS定理可证明△BAE≌△CDF,进而可得结论∠AEB=∠DFC.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠ABE=∠DCF,
∵BE=CF,
∴在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠DCF}\\{EB=CF}\end{array}\right.$,
∴△BAE≌△CDF(SAS),
∴∠AEB=∠DFC.
点评 本题考查了全等三角形的判定和性质,平行四边形的性质,平行线的性质的应用,解题的关键是能将求证角相等的问题转化为寻找其所在的三角形全等,注意:平行四边形的对边互相平行且相等.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.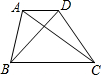 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
 如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )
如图,在梯形ABCD中AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则AD+BC=( )| A. | 20 | B. | 21 | C. | 15 | D. | 24 |
20.甲、乙、丙、丁四位同学都参加了毕业考试前的5次数学模拟测试,每人这5次成绩的平均数都是125分,方差分别S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,测试成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
10.已知对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=2.5 |
 在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.
在平面直角坐标系中,已知两点A(2,0)和M(1,-1),过点M作直线l⊥x轴,直线l上有两动点E和F(点F在点M的上方),且ME=MF.