题目内容
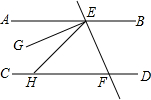 直线AB、CD被EF所截,交点为E、F,H为直线CD上F点左侧的一点,连接HE,满足∠HEF=∠HFE,EG为∠AEH的角平分线,GE⊥EF.求证:AB∥CD.
直线AB、CD被EF所截,交点为E、F,H为直线CD上F点左侧的一点,连接HE,满足∠HEF=∠HFE,EG为∠AEH的角平分线,GE⊥EF.求证:AB∥CD.分析:根据角平分线的定义可得∠AEG=∠HEG,根据垂直定义可得∠HEG+∠HEF=90°,再根据平角等于180°推出∠AEG+∠BEF=90°,然后求出∠BEF=∠HFE,再根据内错角相等,两直线平行即可得证.
解答:证明:∵EG为∠AEH的角平分线,
∴∠AEG=∠HEG,
∵GE⊥EF,
∴∠HEG+∠HEF=90°,∠AEG+∠BEF=180°-90°=90°,
∴∠HEF=∠BEF,
又∵∠HEF=∠HFE,
∴∠BEF=∠HFE,
∴AB∥CD.
∴∠AEG=∠HEG,
∵GE⊥EF,
∴∠HEG+∠HEF=90°,∠AEG+∠BEF=180°-90°=90°,
∴∠HEF=∠BEF,
又∵∠HEF=∠HFE,
∴∠BEF=∠HFE,
∴AB∥CD.
点评:本题主要考查了平行线的判定,关系比较复杂,熟练掌握平行线的判定方法并推出∠BEF=∠HFE是解题的关键.

练习册系列答案
相关题目
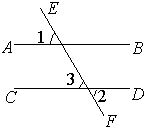 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD, 如图,直线AB,CD被EF所截,下列说法不正确的是( )
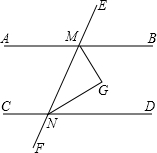
如图,直线AB,CD被EF所截,下列说法不正确的是( ) 如图,已知直线AB,CD被EF所截,MG平分∠EMB,NH平分∠END且MG∥NH,请问AB∥CD吗?为什么?
如图,已知直线AB,CD被EF所截,MG平分∠EMB,NH平分∠END且MG∥NH,请问AB∥CD吗?为什么?