题目内容
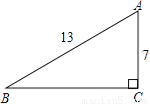
如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB= ．
．
【解析】试题分析：根据锐角三角函数定义直接进行解答．
【解析】
∵在Rt△ABC中，∠C=90°，AB=13，AC=7，
∴sinB==．
故答案为：．
练习册系列答案
相关题目
已知点A的坐标为（-2，3），点B的坐标为（0，1），则点A关于点B的坐标为（ ）
A. （ -2，2 ） B. （2，-3 ） C. （ 2，-1 ） D. （2，3 ）
C
【解析】因为点A的坐标为（-2,3）,点B的坐标为（0,1）,则点A关于点B的坐标为（2,-1）,故选C. 若代数式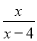
有意义，则实数
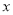的取值范围是（ ）
A. x=0 B. x=4 C. x≠0 D. x≠4
D
【解析】由分式有意义的条件:分母不为0，即x-4≠0，解得x≠4，
故选D. 如图所示，在3×3的正方形网格中已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的办法有
A．3种 B．4种 C．5种 D．6种
C
【解析】
试题分析：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．
选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，
选择的位置有以下几种：1处，3处，7处，6处，5处，选择的位置共有5处
故选C. 如图，在Rt△ABC中，∠C＝90°，AB＝2BC，则sinB的值为 .
【解析】试题分析：因为在Rt△ABC中，∠C = 90°，AB = 2BC，所以． 如图，在塔AB前的平地上选择一点C，测出看塔顶的仰角为30°，从C点向塔底走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为（ ）
A．50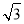
米 B．100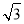米
C．
米 D．
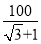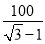米
D.
【解析】
试题解析：在Rt△ABD中，
∵∠ADB=45°，
∴BD=AB．
在Rt△ABC中，
∵∠ACB=30°，
∴=tan30°=，
∴BC=AB．
设AB=x（米），
∵CD=100，
∴BC=x+100．
∴x+100=x
∴x=米．
故选D． Rt△ABC中，∠C=90°，AB=10，BC=8，求cosB的值.
【解析】分析: 直接利用锐角三角函数关系得出cosB.
本题解析：
∵∠C=90°，AB=10，BC=8，
∴cosB=
故答案为： △ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（ ）
A. bcosB=c B. csinA=a C. atanA=b D. tanB＝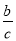
B
【解析】∵a2+b2=c2，
∴△ABC是直角三角形，且∠C=90°，
∴sinA=即csinA=a，
∴B选项正确．
故选B． 计算tan 46°≈_______ ．(精确到0.01)
1.04
【解析】试题解析：tan 46°≈1.0355303138≈1.04.
故答案为：10.4.