题目内容
2.若一个锐角为(5x-15),则x的取值范围是3<x<21.分析 根据锐角三角形的内角的取值列出方程组,然后求解即可.
解答 解:∵锐角三角形中一个锐角为(5x-15)度,
∴$\left\{\begin{array}{l}{5x-15>0①}\\{5x-15<90②}\end{array}\right.$,
解不等式①得,x>3,
解不等式②得,x<21,
所以,x的取值范围是3<x<21.
故答案为:3<x<21.
点评 本题考查了三角形的内角和定理,解一元一次不等式组,理解锐角三角形的内角的范围列出不等式组是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
17.在直角坐标系内,点P(-3,5)关于x轴的对称点P1的坐标为( )
| A. | (3,-5) | B. | (3,5) | C. | (-3,5) | D. | (-3,-5) |
7.下列运算正确的是( )
| A. | a2•a3=a6 | B. | 7a2-a2=7 | ||
| C. | -$(-\frac{1}{2})^{-2}$•(xy2)3=-4x3y6 | D. | (2m-n)2=4m2+n2 |
12.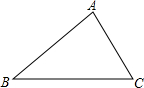 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
 如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )| A. | 作中线AD,再取AD的中点O | |
| B. | 分别作AB、BC的高线,再取此两高线的交点O | |
| C. | 分别作中线AD、BE,再取此两中线的交点O | |
| D. | 分别作∠A、∠B的角平分线,再取此两角平分线的交点O |
 如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N.
如图,点P是正方形ABCD对角线BD上的一点,PM⊥BC,PN⊥DC,垂足分别为M、N. 小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.
小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是58度.
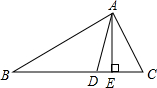 如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.
如图,在△ABC中,已知∠C=60°,∠B=40°,AD是△ABC的角平分线,AE是△ABC的高线,则∠DAE的度数为10°.