题目内容
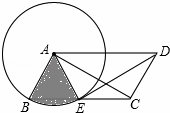
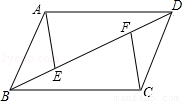
如图,▱ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
考点:
切线的性质;全等三角形的判定与性质;平行四边形的性质;扇形面积的计算.
分析:
(1)由四边形ABCD是平行四边形,AB=AE,易证得四边形AECD是等腰梯形,即可得AC=DE,然后由SSS,即可证得:△AED≌△DCA;
(2)由DE平分∠ADC且与⊙A相切于点E,可求得∠EAD的度数,继而求得∠BAE的度数,然后由扇形的面积公式求得阴影部分(扇形)的面积.
解答:
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴四边形AECD是梯形,
∵AB=AE,
∴AE=CD,
∴四边形AECD是等腰梯形,
∴AC=DE,
在△AED和△DCA中,
 ,
,
∴△AED≌△DCA(SSS);
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵四边形AECD是等腰梯形,
∴∠DAE=∠ADC=2∠AED,
∵DE与⊙A相切于点E,
∴AE⊥DE,
即∠AED=90°,
∴∠ADE=30°,
∴∠DAE=60°,
∴∠DCE=∠AEC=180°﹣∠DAE=120°,
∵四边形ACD是平行四边形,
∴∠BAD=∠DCE=120°,
∴∠BAE=∠BAD﹣∠EAD=60°,
∴S阴影=![]() ×π×22=
×π×22=![]() π.
π.
点评:
此题考查了切线的性质、全等三角形的判定与性质、等腰梯形的判定与性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

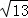 .
.
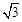 ,则AB的长是
.
,则AB的长是
.