题目内容
如图,▱ABCD中,E,F是对角线BD上两点,且BE=DF.
(1)图中共有 对全等三角形;
(2)请写出其中一对全等三角形: ≌ ,并加以证明.
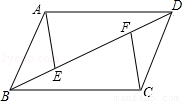
【答案】
解:(1)3。
(2)△ABE,△CDF。证明如下:
∵在▱ABCD中,AB∥CD,AB=CD,∴∠ABE=∠CDF,
∵在△ABE与△CDF中,AB=CD,∠ABE=∠CDF,BE=DF,
∴△ABE≌△CDF(SAS)。
【解析】
试题分析:(1)根据平行四边形的性质和全等三角形的判定定理进行填空:
图中的全等三角形有:△ABE≌△CDF、△ABD≌△CDB、△ADE≌△CBF,共有3对.
(2)根据全等三角形的判定定理SAS可证明△ABE≌△CDF。
另:根据全等三角形的判定定理SSS可证明△ABD≌△CDB:
∵在▱ABCD中,AD=CB,AB=CD,
∴在△ABD与△CDB中,AD=CB,AB=CD,BD=DB,
∴△ABD≌△CDB(SSS)。
根据全等三角形的判定定理SAS可证明△ADE≌△CBF:
∵在▱ABCD中,AD∥BC,AD=CB,∴∠ADE=∠CBF。
∵BE=DF,∴DE=BF。
∵在△ADE与△CBF中,AD=CB,∠ADE=∠CBF, DE=BF,
∴△ADE≌△CBF(SAS)。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

 .
.
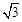 ,则AB的长是
.
,则AB的长是
.