题目内容
已知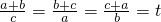 ,那么直线f(x)=tx+t一定通过第________象限.
,那么直线f(x)=tx+t一定通过第________象限.
二、三
分析:可分a+b+c=0和a+b+c≠0两种情况代入求值和利用等比性质求得t可能的值,进而根据一次函数图象的性质得到一定经过的象限.
解答:①当a+b+c=0时,
b+c=-a,c+a=-b,a+b=-c,
∴t为其中任何一个比值,即t=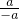 =-1,此时直线f(x)=tx+t通过二、三、四象限;
=-1,此时直线f(x)=tx+t通过二、三、四象限;
②a+b+c≠0时,
t=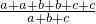 =2,此时直线f(x)=tx+t通过一、二、三象限;
=2,此时直线f(x)=tx+t通过一、二、三象限;
∴直线f(x)=tx+t一定通过第 二、三象限,
故答案为:二、三.
点评:考查比例性质的应用及一次函数图象的性质;分类探讨出t可能的值是解决本题的突破点;用到的知识点为:一次函数的比例系数,常数项均大于0,图象经过一、二、三象限;一次函数的比例系数,常数项均小于0,图象经过二、三、四象限.
分析:可分a+b+c=0和a+b+c≠0两种情况代入求值和利用等比性质求得t可能的值,进而根据一次函数图象的性质得到一定经过的象限.
解答:①当a+b+c=0时,
b+c=-a,c+a=-b,a+b=-c,
∴t为其中任何一个比值,即t=
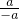 =-1,此时直线f(x)=tx+t通过二、三、四象限;
=-1,此时直线f(x)=tx+t通过二、三、四象限;②a+b+c≠0时,
t=
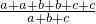 =2,此时直线f(x)=tx+t通过一、二、三象限;
=2,此时直线f(x)=tx+t通过一、二、三象限;∴直线f(x)=tx+t一定通过第 二、三象限,
故答案为:二、三.
点评:考查比例性质的应用及一次函数图象的性质;分类探讨出t可能的值是解决本题的突破点;用到的知识点为:一次函数的比例系数,常数项均大于0,图象经过一、二、三象限;一次函数的比例系数,常数项均小于0,图象经过二、三、四象限.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知C是直线AB上一点,且
=
,那么下列结论中,正确的是( )
| AC |
| 1 |
| 2 |
| BC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 (2012•常州模拟)在直角坐标系中,已知A(0,1),B(10,1),C(9,4).
(2012•常州模拟)在直角坐标系中,已知A(0,1),B(10,1),C(9,4). 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.