题目内容
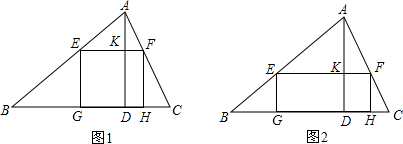
18.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
分析 (1)根据矩形的对边平行得到BC∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”判定即可.
(2)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,根据EF∥BC,得到△AEF∽△ABC,根据相似三角形的性质得到比例式,解方程即可得到结果;
(3)根据矩形面积公式得到关于x的二次函数,根据二次函数求出矩形的最大值.
解答 解:(1)∵四边形EGFH为矩形,
∴BC∥EF,
∴△AEF∽△ABC;
(2)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,
∵EF∥BC,
∴△AEF∽△ABC,
∵AD⊥BC,
∴$\frac{EF}{BC}=\frac{AK}{AD}$,
∴$\frac{x}{120}=\frac{80-x}{80}$,
解得x=48.
答:正方形零件的边长为48mm.
(3)设EF=x,EG=y,
∵△AEF∽△ABC
∴$\frac{EF}{BC}=\frac{AK}{AD}$,
∴$\frac{x}{120}$=$\frac{80-y}{80}$
∴y=80-$\frac{2}{3}$x
∴矩形面积S=xy=-$\frac{2}{3}$x2+80x=-$\frac{2}{3}$(x-60)2+2400(0<x<120)
故当x=60时,此时矩形的面积最大,最大面积为2400mm2.
点评 本题考查了正方形以及矩形的性质,结合了平行线的比例关系求解,注意数形结合的运用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
9.一个多边形的内角和是外角和的2倍,这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
13.下列各图中,∠1与∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
3.人体血液中每个成熟红细胞的平均直径为0.0000077米,用科学记数法表示为( )
| A. | 7.7×10-5米 | B. | 77×10-6米 | C. | 77×10-5米 | D. | 7.7×10-6米 |
7.以下列各组数为边长,不能构成直角三角形的是( )
| A. | 5,12,13 | B. | 9,12,15 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | D. | 0.3,0.4,0.5 |