题目内容
（1）如图，在矩形ABCD中，BF=CE，求证：AE=DF；
（2）如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，求∠BCD的度数．
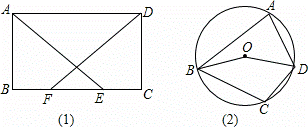
（1）证明：∵四边形ABCD是矩形，
∴AB=CD，∠B=∠C=90°，
∵BF=CE，
∴BE=CF，
在△ABE和△DCF中
∴△ABE≌△DCF，
∴AE=DF；
（2）解：∵∠BOD=160°，
∴∠BAD= 
∠BOD=80°，
∵A、B、C、D四点共圆，
∴∠BCD+∠BAD=180°，
∴∠BCD=100°．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
的解集在数轴上可表示为（ ）
B．
C．
D．
D在同一直线上)．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据：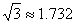
，
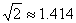．结果保留整数）．