题目内容
3.在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是多少?分析 根据线段垂直平分线性质求出AE=BE,根据勾股定理求出AE即可.
解答 
解:∵AB的垂直平分线交AB于点D,交BC于点E,
∴BE=AE,
∵在Rt△ACE中,CE=5,AC=12,∠C=90°,由勾股定理得:AE=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴BE=AE=13.
点评 本题考查了线段垂直平分线性质,勾股定理的应用,能根据线段垂直平分线性质求出AE=BE是解此题的关键,注意:线段垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
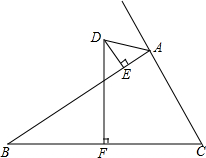 如图,在△ABC中,AB>AC,BC的垂直平分线DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,线段AC,AE,BE之间有怎样的关系?请写出你的猜想,并加以证明.
如图,在△ABC中,AB>AC,BC的垂直平分线DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,线段AC,AE,BE之间有怎样的关系?请写出你的猜想,并加以证明. 如图,四边形ABCD中,DA=DB=DC,∠ADC=110°,求∠ABC的度数.
如图,四边形ABCD中,DA=DB=DC,∠ADC=110°,求∠ABC的度数. 已知:如图.在平行四边形ABCD中,点E、F分别是AB、DC的中点.求证:四边形BDEF是平行四边形.
已知:如图.在平行四边形ABCD中,点E、F分别是AB、DC的中点.求证:四边形BDEF是平行四边形.