题目内容
10.解方程组$\left\{\begin{array}{l}{\frac{2x-5}{x-2}+\frac{2y-3}{y-1}=2}\\{3x-4y=1}\end{array}\right.$.分析 方程组第二个方程变形表示出y,代入第一个方程得到关于x的分式方程,求出分式方程的解得到x的值,进而求出y的值,经检验即可得到方程组的解.
解答 解:$\left\{\begin{array}{l}{\frac{2x-5}{x-2}+\frac{2y-3}{y-1}=2①}\\{3x-4y=1②}\end{array}\right.$,
由②得:y=$\frac{3x-1}{4}$③,
③代入①得:$\frac{2x-5}{x-2}$+$\frac{\frac{3x-1}{2}-3}{\frac{3x-1}{4}-1}$=2,
整理得:$\frac{2x-5}{x-2}$+$\frac{6x-14}{3x-5}$=2,
去分母得:6x2-25x+25+6x2-26x+28=6x2-22x+20,即6x2-29x+33=0,
分解得:(6x-11)(x-3)=0,
解得:x=$\frac{11}{6}$或x=3,
把x=$\frac{11}{6}$代入②得:y=$\frac{9}{8}$;把x=3代入②得:y=2,
经检验$\left\{\begin{array}{l}{x=\frac{11}{6}}\\{y=\frac{9}{8}}\end{array}\right.$与$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$都为原方程组的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列命题中正确的是( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似.
| A. | ①③ | B. | ①④ | C. | ①②④ | D. | ①③④ |
1.在下列四个一元二次方程中,没有实数根的一个是( )
| A. | x2-8x+1=0 | B. | 2x2+1=3x | C. | 3x2-6x+4=0 | D. | (x-2)2-1=0 |
 拦水坝横断面如图所示,迎水坡AB的坡比是1:$\sqrt{3}$,坝高BC=10m,则坡面AB的长度是20m.
拦水坝横断面如图所示,迎水坡AB的坡比是1:$\sqrt{3}$,坝高BC=10m,则坡面AB的长度是20m.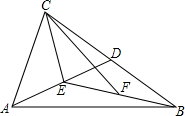 如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.
如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.