题目内容
20. 若不等式组$\left\{\begin{array}{l}{x-a+b<0}\\{x+a+b>0}\end{array}\right.$的解集的数轴表示如图,
若不等式组$\left\{\begin{array}{l}{x-a+b<0}\\{x+a+b>0}\end{array}\right.$的解集的数轴表示如图,(1)用不等式表示这个不等式组的解集;
(2)求a,b的值.
分析 (1)解不等式组,即可解答;
(2)根据数轴可知不等式的解集为:1<x<6,所以 $\left\{\begin{array}{l}{-a-b=1}\\{a-b=6}\end{array}\right.$,解方程组即可解答.
解答 解:(1)不等式组$\left\{\begin{array}{l}{x-a+b<0}\\{x+a+b>0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x<a-b}\\{x>-a-b}\end{array}\right.$
∴不等式组的解集为:-a-b<x<a-b.
(2)由数轴可知不等式的解集为:1<x<6,
∴$\left\{\begin{array}{l}{-a-b=1}\\{a-b=6}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=2.5}\\{b=-3.5}\end{array}\right.$.
点评 本题考查了在数轴上表示不等式的解集,解决本题的关键是解不等式组.

练习册系列答案
相关题目
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
10.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
| A. | 有一个内角小于90° | B. | 有一个内角小于或等于90° | ||
| C. | 每一个内角都小于90° | D. | 每一个内角都大于90° |
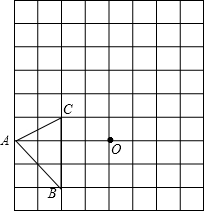 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算: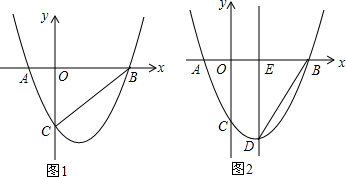
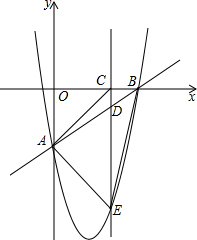 如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.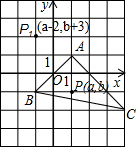 如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.
如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1. 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.