题目内容
设方程ax2+bx+c=0(a≠0)的两根之比为2:3.求证:6b2=25ac分析:先设方程ax2+bx+c=0(a≠0)的两根是2α,3α,根据根与系数的关系可得2α+3α=-
,2α•3α=
,从2α+3α=-
可求出α,再把α的值代入2α•3α=
中,化简即可.
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
解答:解:设方程ax2+bx+c=0(a≠0)的两根是2α,3α,则
2α+3α=-
,2α•3α=
,
∴5α=-
①,6α2=
②,
由①得α=-
③,
把③代入②,得
6×(-
)2=
,
即
=
,
∴25a2c=6ab2,
∴25ac=6b2.
2α+3α=-
| b |
| a |
| c |
| a |
∴5α=-
| b |
| a |
| c |
| a |
由①得α=-
| b |
| 5a |
把③代入②,得
6×(-
| b |
| 5a |
| c |
| a |
即
| 6b2 |
| 25a2 |
| c |
| a |
∴25a2c=6ab2,
∴25ac=6b2.
点评:此题主要考查了根与系数的关系、比例的性质,若x1、x2是方程ax2+bx+c=0的两根,则有x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
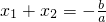 ,
,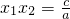 .根据该材料填空:若关于x的一元二次方程x2-(n+2)x-2n2=0的两根记作an、bn(n为不小于2的整数),则
.根据该材料填空:若关于x的一元二次方程x2-(n+2)x-2n2=0的两根记作an、bn(n为不小于2的整数),则 …
… =________.
=________.