题目内容
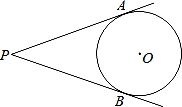
如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为 .
70°或110° .
【考点】切线的性质.
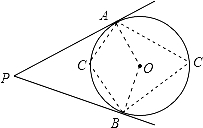
【分析】首先连接OA、OB,在AB弧上任取一点C,连接AC、BC,由PA、PB是⊙O的切线,根据切线的性质,可得∠OAP=∠OBP=90°,又由∠APB=40°,即可求得∠AOB的度数,然后分别从①若C点在优弧AB上与②若C点在劣弧AB上去分析,即可求得∠ACB的度数.
【解答】解:连接OA、OB,在AB弧上任取一点C,连接AC、BC,
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∵∠APB=40°,
∴在四边形OAPB中,∠AOB=360°﹣∠APB﹣∠OAP﹣∠OBP=140°.
①若C点在优弧AB上,则∠ACB=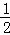 ∠AOB=70°;
∠AOB=70°;
②若C点在劣弧AB上,则∠ACB=180°﹣70°=110°,
故答案为:70°或110°.
【点评】此题主要考查了切线的性质与圆周角的性质,解题的关键是注意数形结合思想与分类讨论思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
 (x+1)2+3,下列结论不正确的是( )
(x+1)2+3,下列结论不正确的是( ) .分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为
.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为 

 B.k<
B.k< = .
= .
 ;
;